ERDC/CHL CETN-IV-25
June 2000
1 E -1
deepw ater asym ptote
for blocking
1 E -2
shallow w ater asym ptote
for blocking
1 E -3
1 E -4
1 E -7
1 E -6
1 E -5
1 E -4
1 E -3
1 E -2
1 E -1
1E +0
R e la tiv e W a te r D e p th (d/L o )
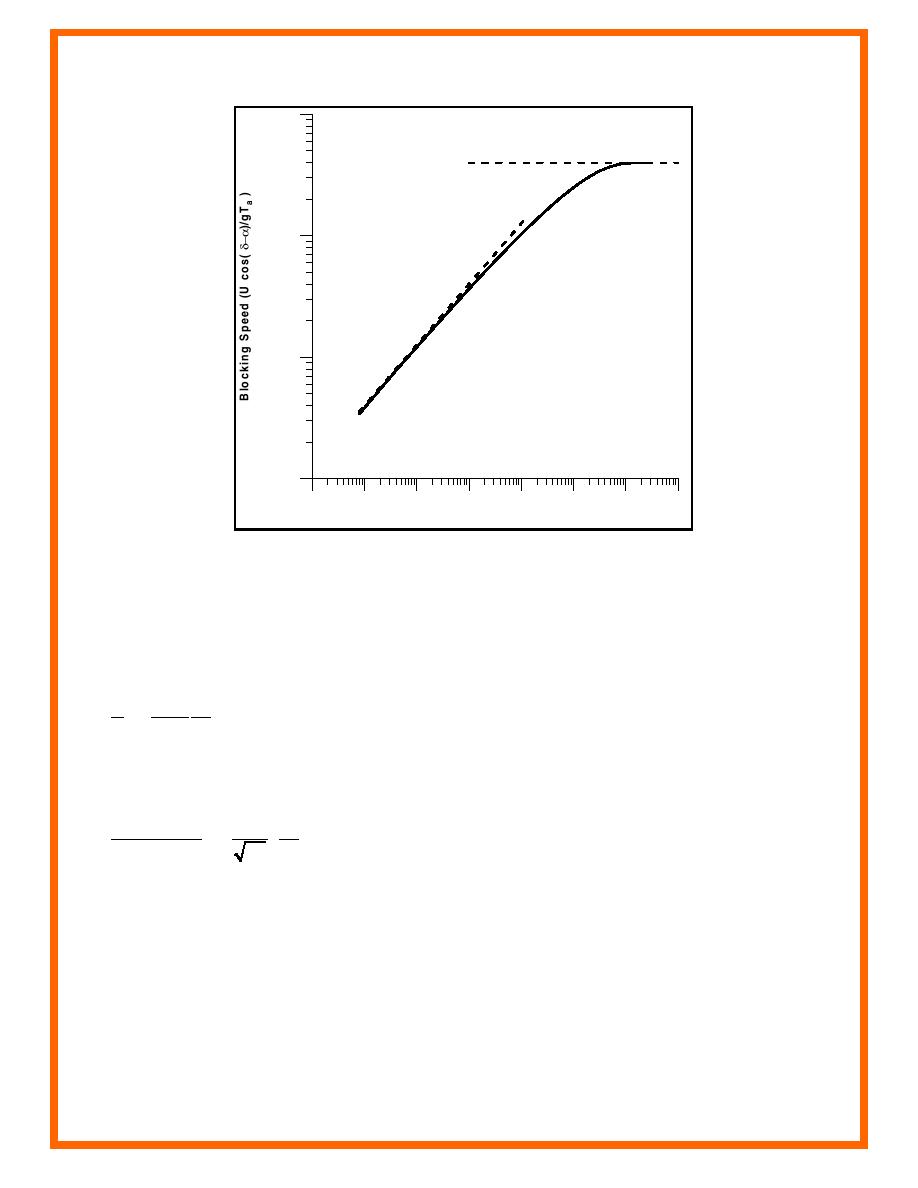
Figure 2. Non-dimensional blocking speed as a function
of relative water depth
where Co is the phase speed in deep water neglecting the current (=gTa/2π). In shallow water, kd
the wavelength at blocking:
1/ 6
d 9 d
=
(19)
L 32π5 Lo
The corresponding current speed at blocking is given by:
1/ 2
1 d
U cos(δ - α)
=-
(20)
2π Lo
gTa
This relationship is in fact identical to U cos(δ-α)=(gd)1/2. The asymptotes for deep and shallow
water are indicated in Figure 2.
The wave equations are numerically solved by a finite-difference formulation similar to that in
NMLONG. For representing waves with random height, a Monte-Carlo simulation is carried out
for a large number of individual waves belonging to the Rayleigh probability density distribution
in the offshore so that statistically stable wave quantities are obtained in averaging the results
from all the waves. The Rayleigh distribution will not necessarily be followed as the waves
propagate onshore and break or are modified by the current-wave interaction. Because the wave
6



 Previous Page
Previous Page
