ERDC/CHL CHETN-II-45
March 2002
1.5
Model=Predicted
dA
SH
A
1.0
0.5
RMSE-dA=0.190
RMSE-SH=0.105
RMSE-A=0.102
0.0
0.0
0.5
1.0
1.5
Kt Model Results
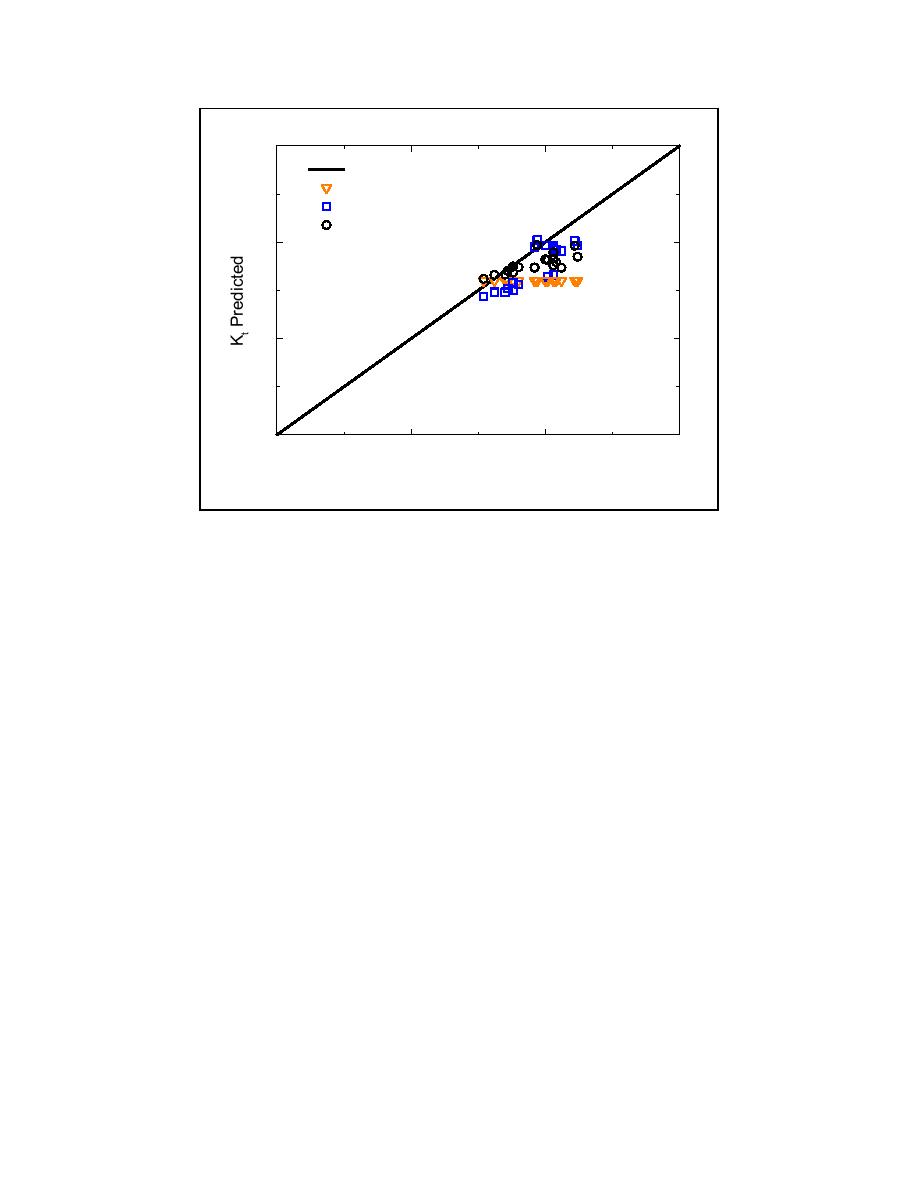
Figure 7. Transmission coefficient predictions and Boussinesq model results
Wave transmission data were also collected at three locations along the spur for three different
offshore wave conditions in a 3-D physical model being operated at the U.S. Army Engineer
Waterways Experiment Station of the Grays Harbor site with the spur in place. Waves were
created in the 1:75 scale model with a 24-m-long plunger-type wave generator. The generator
was programmed with actual prototype wave spectrum information to recreate the scaled waves.
Each wave condition was run at mllw, mtl, and mean high water (mhw). The transmission data
collected at the three measurement locations along the spur were averaged and are compared to
the d'Angremond, Seabrook and Hall, and Ahrens formulations in Figure 8. The Ahrens
equation again gives best agreement. The Seabrook and Hall equation also compares well to the
physical model data, whereas the d'Angremond results again invoked the upper limit for many
wave conditions. The d'Angremond equation is not applicable for this situation of high relative
submergence.
The high submergence, large incident wave heights, and small stone size for the Grays Harbor
spur place it close to the stated variable range limits for the Seabrook and Hall equation. In this
situation, applicability of this equation is questionable for the larger wave heights. Predicted
transmission coefficients from the Ahrens and the Seabrook and Hall equations are plotted in
Figure 9 versus wave height for constant water level. The Ahrens formulation indicates a
reduction in Kt with increasing wave height. The smaller waves shoal on the submerged spur,
The Seabrook and Hall formulation also displays a decreasing Kt with increase in incident wave
height for Hs < 4m. The Seabrook and Hall formulation then yields Kt values that increase with
increase in wave height. The unexpected results begin to occur if the Seabrook and Hall
equation is applied outside the range of their stated test parameters. Based on these results, it
9



 Previous Page
Previous Page
