ERDC/CHL CHETN-IV-34
June 2001
2
2
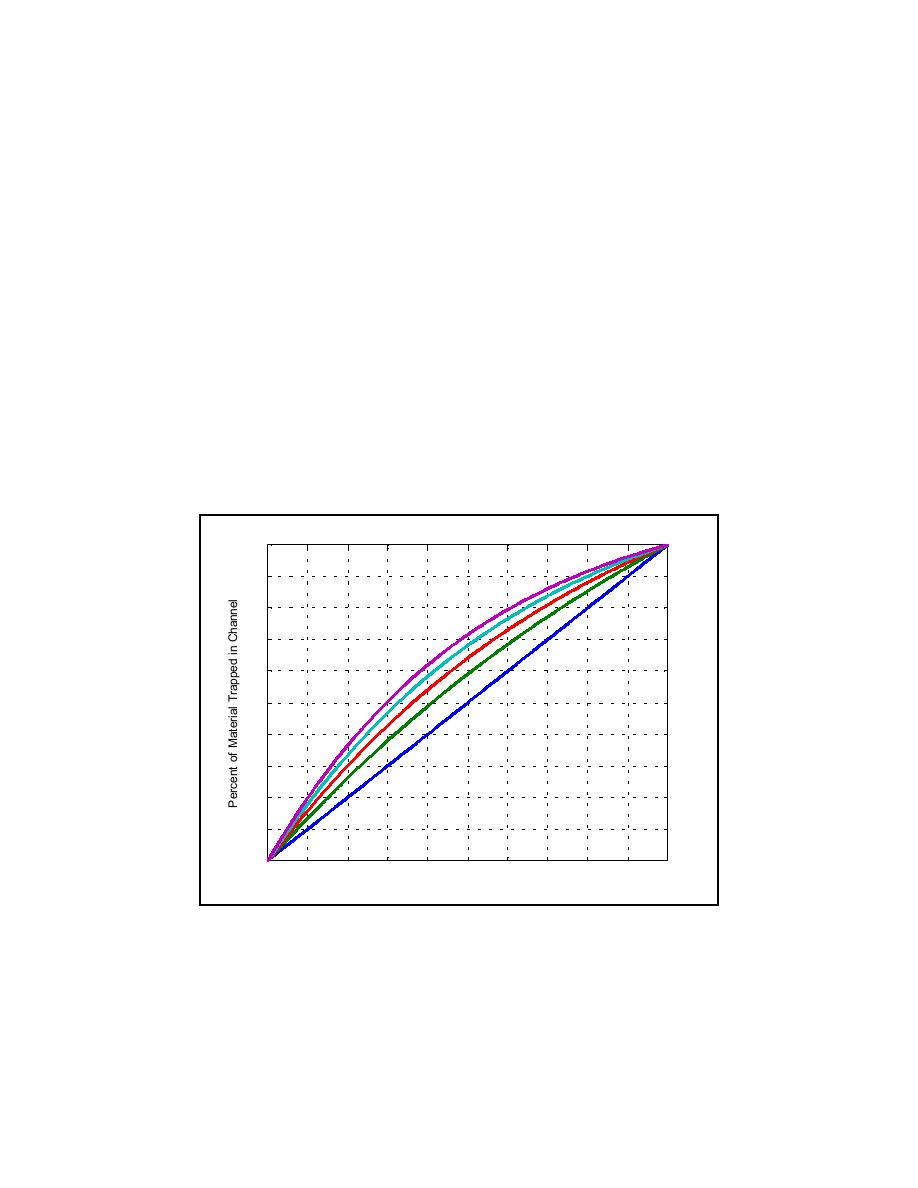
p = hcWV f /(haU a ) . If the calculated value of hcWV f /(haU a ) is larger than 1, then p = 1, and all
material will fall into the channel.
If p-percent of the suspended material at a given instant is trapped in the channel, then (1-p)
percent bypasses the channel by being advected over it. Kraus and Larson (2001) describes how
material may also be resuspended and transported out of a channel, thereby increasing the
amount bypassed.
The depth-averaged current velocity perpendicular to the channel should be employed for
predicting the trapping ratio. If the current approaches the channel at an angle θ with respect to
the orientation of the channel (i.e., for a perpendicular current θ = 90 deg), the current should be
divided by sin θ before it inserted as Ua in Equation 7. This result indicates that the trapping
ratio increases because the distance traveled for the sediment particles across the channel
becomes longer (or equivalently, the component of the incident current transporting the particles
across the channel becomes smaller). If there is a uniform current along the channel axis during
its crossing of the channel, the end result of consideration of the processes is that there is no
change in the trapping ratio. Although, the distance the sediment particles travel increases, so
does the speed, and the two processes cancel.
9I
JKD
)U
)U
9I8D
:KD
KFKD
Figure 3. Percentage of sediment falling into the channel
EXAMPLES: The preceding development provides a means of estimating the percentage of
suspended material that may fall into a channel (or which may bypass a channel) based on
sediment fall speed, geometry of the channel, and the speed of the upstream flow crossing the
channel. Here, two examples are given to illustrate applications of this information.
6



 Previous Page
Previous Page
