CETN IV-15
Rev. September 1999
There are numerous ways of formulating a sediment budget (e.g., Shore Protection Manual
1984; Jarrett 1991; Bodge 1999; Mann 1999). The difference between the sediment sources and
the sinks in each cell, hence for the entire sediment budget, must equal the rate of change in
sediment volume occurring within that region, accounting for pertinent engineering activities.
The sediment budget equation can be expressed as,
∑Q
- ∑ Qsink - ∆V + P - R = Residual
(1)
source
in which all terms are expressed consistently as a volume or as a volumetric change rate; Qsource
and Qsink are the sources and sinks to the control volume, respectively; V i s the net change in
volume within the cell; P and R are the amounts of material placed in and removed from the cell,
respectively; and Residual represents the degree to which the cell is balanced. For a balanced
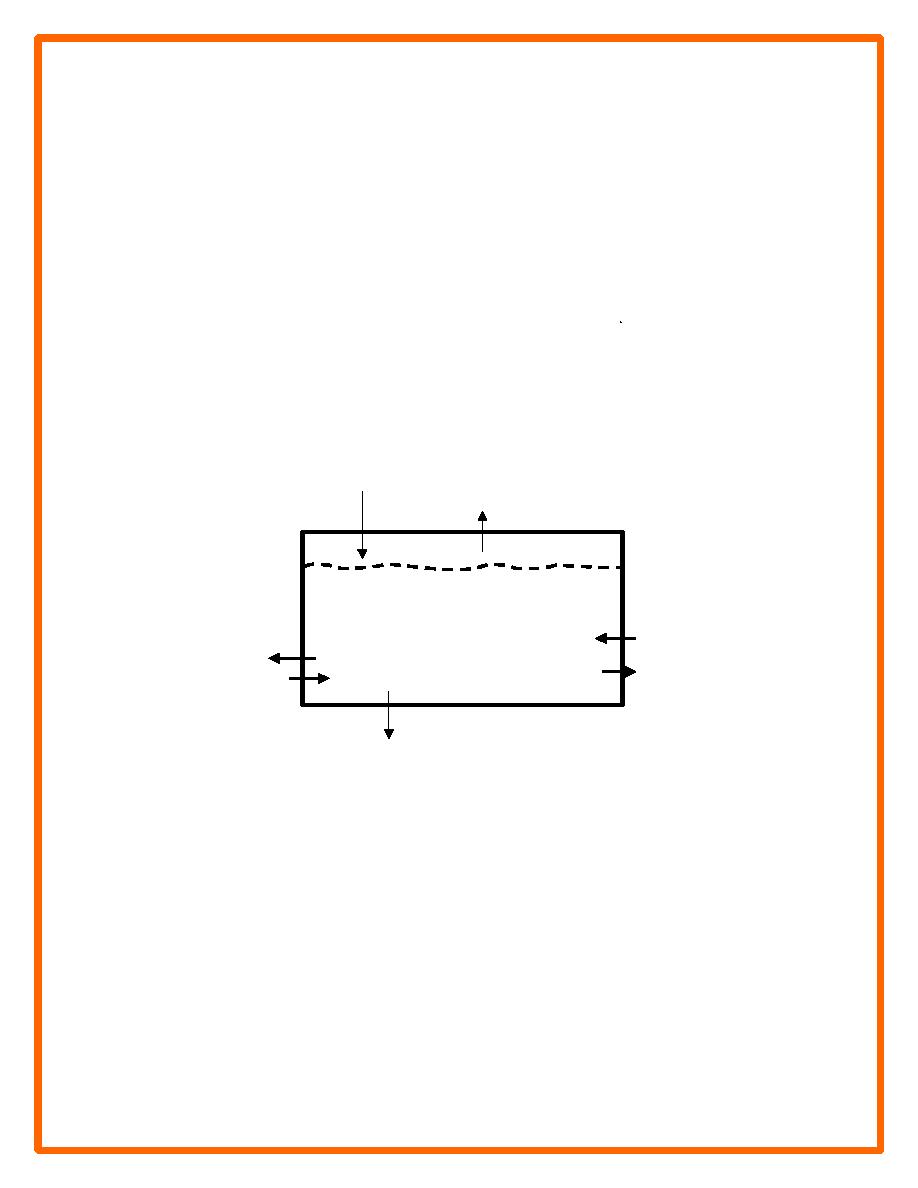
cell, the residual is zero. Figure 1 schematically illustrates the parameters appearing in
Equation 1. For a reach of coast consisting of many contiguous cells, the budget for each cell
must balance in achieving a balanced budget for the entire reach.
Qsource (e.g., bluffs, river influx)
Qsink (e.g., wind-blown transport)
beach
∆V (beach erosion/accretion),
P (beach fill, dredged placement), Q
Qsink (LST)
source (LST)
R (dredging, mining)
Qsource (LST)
Qsink (LST)
ocean
Qsink (e.g., sea level, submarine canyon)
Figure 1. Sediment budget parameters as may enter Equation 1
As noted in Figure 1, sources to the sediment budget include longshore sediment transport,
erosion of bluffs, transport of sediment to the coast by rivers, erosion of the beach, beach fill and
dredged material placement, and a decrease in relative sea level. Examples of sediment budget
sinks are longshore sediment transport, accretion of the beach, dredging and mining of the beach
or nearshore, relative sea-level rise, and losses to a submarine canyon.
If inlets are located within the domain of a coastal sediment budget, they present significant
challenges because inlets and the adjacent beaches are connected. Inlets increase the complexity
of sediment budgets for several reasons. First, sediment-transport magnitudes and pathways are
difficult to define at inlets, even in a relative sense. Flood and ebb currents, combined waves and
currents, wave refraction and diffraction over complex bathymetry, and engineering activities
complicate transport rate directions and may increase or decrease their magnitudes. Because the
pathways of sediment movement in the vicinity of an inlet can be circuitous, equations
2



 Previous Page
Previous Page
